An Interesting Kinematics Problem
I was reviewing kinematics (for fun, of course) because its my favorite physics topic because of its extreme relevance to the real world. After all, who hasn’t dropped something or pushed something off a table. I was grinding some problems and came across a really interesting one.
Problem
A rabbit begins at the origin and a fox begins at (0, -a). At $t=0$, the rabbit begins moving with velocity $\boldsymbol{v}_r = v \boldsymbol{\hat{x}}$. Simultaneously, the fox begins running directly after the rabbit with speed $v$. Find the distance betwen the animals after a long time.
Diagram
It’s important to make a diagram in these kinds of problems, as you can easily get lost in the coordinates, directions, etc. We draw a diagram using Asymptote, mostly because it looks really nice. This diagram shows the system at some point in time $t$.
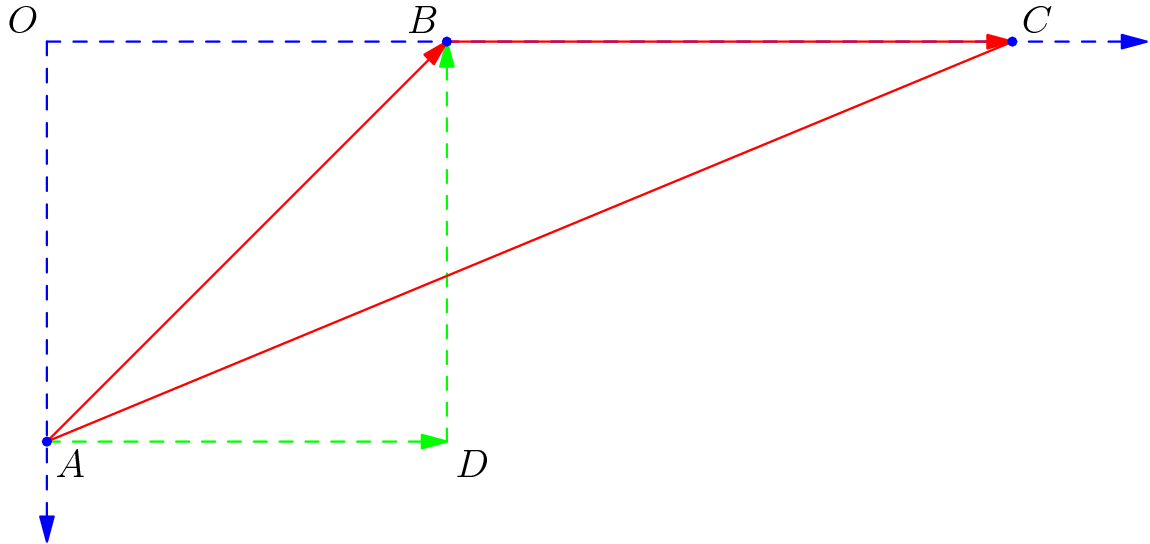
We also need to do some geometry (see next section). Let $O$ be the origin. Let $A$ be the position of the fox. Let $B$ be the position of the rabbit. Let $C$ be the intersection of the velocity vectors when extended outwards (this isn’t really physically relevant, but we use it later). Let $D$ be the interesection of the horizontal and vertical components of the fox’s velocity (also not physically relevant, but we also use it later).
Some Geometry
We start with some angle-chasing. Let $\angle ABC \equiv \theta$. By definition of components, $\overline{DB} \perp \overline{AD}$, so $\angle ABD = \theta - \frac{\pi}{2}$. By complementary angles, $\angle BAD = \frac{\pi}{2} - \angle ABD = \pi - \theta $. Let $r \equiv \overline{AB}$ and $x \equiv \overline{AD}$.
Critical Lemma
We seek to show that throughout the motion, $r+x$ is conserved.
Consider the frame of the rabbit. In this frame, the fox’s horizontal velocity is $ v \cos{\theta}$. Therefore,
\[\frac{dx}{dt} = v \cos{\theta} - v\]Now consider the frame of the fox. In this frame, the rabbit is running away at speed $- v \cos{\theta}$, so
\[\frac{dr}{dt} = v - v \cos{\theta}\]Adding the two, we see that $\frac{d}{dt} \left (r+x \right) = 0$
Implying that the quantity is conserved.
Solution
Initially, $r+x = a$. After a time $t \gg \frac{a}{v}$ has passed, there is effectively no vertical distance, so $r = x = \frac{a}{2}$.
Notice that we used a conservation law here. Usually, we would have used a standard conservation law, like conservation of energy or momentum, but instead, we madee our own conservation law. ༼ʘ̚ل͜ʘ̚༽ ᕦ(ò_óˇ)ᕤ Just like mathematics, creativity in physics helps a lot. Coming up tomorrow: Chapter 2 of Plasma Physics! (͡ ͡° ͜ つ ͡͡°) See you tomorrow, I’ve got HW to do! (☞ຈل͜ຈ)☞