A USAPhO Problem
Today, we will be doing one of my favorite problems of all time: USAPhO 2011 A2!.
Solution
First, we find the moment of inertia, using the parallel axis theorem. Since the stick is suspended a distance $R$ away from the center, we can write the moment of intertia as
\[I = \frac{1}{12} ML^2 + MR^2\]Next, we can compute the torque about this axis.
\[\tau = -mgR \sin{\theta} \approx -mgR \theta\]Using Newton’s Second Law for rotational motion, we can write the equation
\[\left (\frac{1}{12} ML^2 + MR^2 \right) \ddot{\theta} = - mgR \theta \Rightarrow \ddot{\theta} = - \frac{12gR}{L^2 + 12R^2} \theta\]This equation of motion is in the form of a simple harmonic oscillator, so we can simply write down that its period is
\[T = 2 \pi \sqrt{\frac{L^2 + 12 R^2}{12gR}}\]To use the data we are provided, we must turn this into a linear equation that can be plotted. Doing some algebraic manipulation on this equation, we get
\[T^2 R = \frac{12 \pi^2 R^2}{3g} + \frac{\pi^2 L^2}{3g}\]This indicates that we can plot $R^2$ on the x-axis and $T^2 R$ on the y-axis. If we do so, we will find that the slope will be
\[m = \frac{12 \pi^2}{3g}\]Similarly, the y-intercept of the line will be
\[b = \frac{\pi^2 L^2}{3g}\]We first compute $R^2$ and $T^2 R$ for each data point given and report the results below, using an appropriate number of significant figures.
| $R^2$ (m^2) | $T^2 R$ (m/s^2) |
|---|---|
| 0.0025 | 0.74 |
| 0.0056 | 0.75 |
| 0.0104 | 0.770 |
| 0.0243 | 0.826 |
| 0.0392 | 0.886 |
| 0.0445 | 0.908 |
| 0.0912 | 1.10 |
| 0.150 | 1.33 |
| 0.203 | 1.55 |
| 0.346 | 2.12 |
To graph this, we use Asymptote, because it looks cool and because we can. I’ve also included the code below, in case you wanted to tinker with the display.
[asy]
unitsize(150);
draw((0,0) -- (2,0), arrow=Arrow(HookHead), blue);
draw((0,0) -- (0, 2), arrow = Arrow(HookHead), blue);
label("$0$", (0, 0), SW, olive);
label("$R^2$", (2, 0), E, green);
label("$T^2R$", (0, 2), N, green);
real[] X = {0.0025, 0.005625, 0.010404, 0.024336, 0.039204, 0.044521, 0.091204, 0.149769, 0.203401, 0.345744};
real[] Y = {0.7380482, 0.7508172, 0.769692918, 0.825957756, 0.88569855, 0.907611436, 1.09596555, 1.331676675, 1.548557659, 2.12268};
for(int i = 0; i < 9; ++i)
{
dot((X[i], Y[i]), red);
}
real sumProducts = 0;
real sumX = 0;
real sumY = 0;
real sumXSquare = 0;
int N = 10;
for(int i = 0; i < 9; ++i)
{
sumProducts += X[i] * Y[i];
sumX += X[i];
sumY += Y[i];
sumXSquare += X[i]^2;
}
real m = (N * sumProducts - sumX * sumY)/(N * sumXSquare - sumX^2);
real b = (sumY - m * sumX)/(N);
real f(real x)
{
return m * x + b;
}
path g = graph(f, 0, 0.27);
draw(g, arrow = Arrow(HookHead));
[/asy]
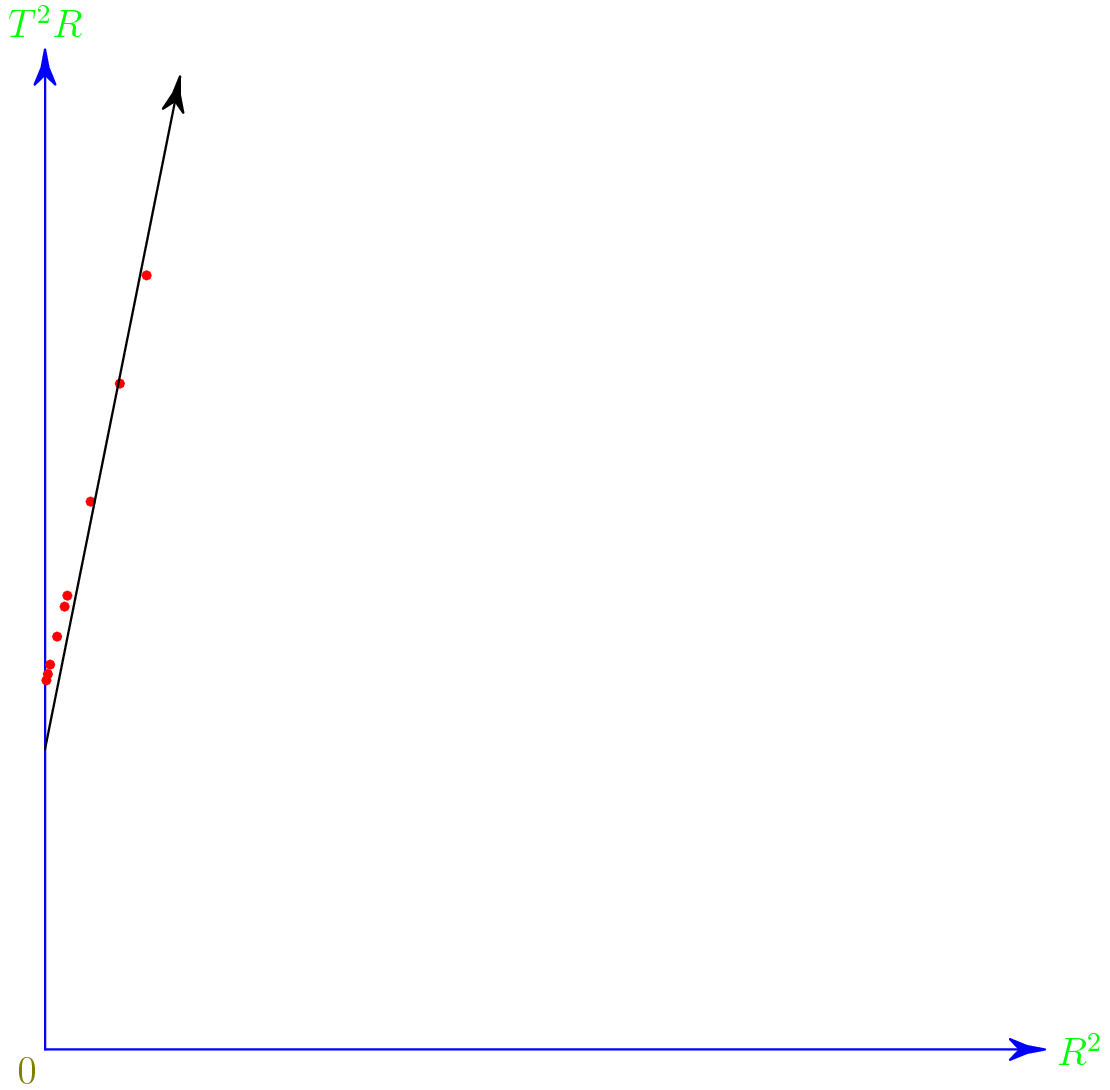
We see that $m = 4.09$ and $b = 0.713$. Solving the equations above, we see that
\[g = \frac{12 \pi^2}{3m} = \frac{12 \pi^2}{3 (4.09)} = 9.65\ \frac{\text{m}}{\text{s}^2}\] \[L = \sqrt{\frac{12b}{m}} = \sqrt{\frac{12 (0.713)}{(4.09)}} = 1.45\ \text{m}\]