A Nice(ish) Eigenvalue Problem
So I came across a problem when I was doing some EM that I want to share with you today.
Problem (BAUPC 1997)
Consider a region of space in which there is a magnetic field $\vec{B} = B \vec{\hat{z}}$. A particle of charge $q$ and mass $m$ is given an initial velocity $\vec{v}_0 = v_0 \vec{\hat{y}}$. Find the final position of the particle if it is also subject to a damping force $\vec{F} = - \alpha \vec{v}$.
My Solution
First off, a disclaimer: this won’t be the most elegant solution, but the most mathematically satisfying one. As always, there are multiple ways to do this problem. The most efficient way is to guess some sinusoidal motion with damping, and solving for the frequencies and coeffiecients.
Let’s start by finding the magnetic force. Denote the velocity vector by $\vec{v} = v_x \vec{\hat{x}} + v_y \vec{\hat{y}} + v_z \vec{\hat{z}}$. Magnetic force is given by $\vec{F} = q \vec{v} \times \vec{B}$. Evaulating the cross products, or using the right hand rule, we can see that the force in the $\vec{\hat{z}}$-direction vanishes. Therefore, we only need to consider the x and y-directions in order to use Newton’s Second Law. We can’t use conservation of energy here because both the magnetic force is perpendicular to the velocity, resulting in 0 work being done by it. Moreover, both forces are nonconservative.
Using Newton’s Second Law in the x-direction,
\[\dot{v_x} = \frac{qB}{m} v_y - \frac{\alpha}{m} v_x\]and in the y-direction,
\[\dot{v_y} = - \frac{qB}{m} v_x - \frac{\alpha}{m} v_y\]This is a system of differential equations, so we use the method of normal modes, arising from linear algebra. We start by guessing a solution in the form of
\[\vec{v} = \begin{pmatrix} A_1 \\ A_2 \\ \end{pmatrix} e^{\lambda t}\]Subsituting, we find the following matrix equation:
\[\begin{pmatrix} \lambda + \frac{\alpha}{m} & - \frac{qB}{m} \\ \frac{qB}{m} & \lambda + \frac{\alpha}{m} \\ \end{pmatrix} \begin{pmatrix} A_1 \\ A_2 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \end{pmatrix}\]In order to have nontrivial values for $A_1$ and $A_2$, we require that the left matrix be non-invertible. One way it can be non-invertible is if the determinant is 0. Setting it equal to $0$ and solving, we find two solutions, which are the eigenvalues of the matrix, which we denote $\lambda_1$ and $\lambda_2$.
\[\lambda_1 = -\frac{\alpha}{m} + i \frac{qB}{m}\] \[\lambda_2 = - \frac{\alpha}{m} - i \frac{qB}{m}\]The eigenvectors can be found by substituting the eigenvalues into the matrix and using Gaussian elimination to solve for $A_1$ and $A_2$. Let the respective eigenvectors be $\vec{e}_1$ and $\vec{e}_2$.
\[\vec{e}_1 = \begin{pmatrix} - i \\ 1 \\ \end{pmatrix}\] \[\vec{e}_2 = \begin{pmatrix} i \\ 1 \\ \end{pmatrix}\]Now is the fun (acquired taste ¯_(ツ)_/¯) part. Using the eigenvalues and eigenvectors we solved for, we can say that the general solution for the velocity will be in the form
\[\vec{v}(t) = C_1 \begin{pmatrix} - i \\ 1 \\ \end{pmatrix} e^{\left (- \frac{\alpha}{m} + i \frac{qB}{m} \right)t} + C_2 \begin{pmatrix} i \\ 1 \\ \end{pmatrix} e^{\left (- \frac{\alpha}{m} - i \frac{qB}{m} \right)t}\]We can solve for the initial conditions to find that
\[\vec{v}(t) = v_0 e^{- \frac{\alpha}{m} t} \begin{pmatrix} \sin{\left (\frac{qB}{m} t\right)} \\ \cos{\left (\frac{qB}{m} t\right)} \\ \end{pmatrix}\]To find the displacement from the origin, we integrate (to avoid integrating by parts, convert both components into complex exponentials) this vector with respect to time, and find
\[\vec{r} = \frac{m^2 v_0}{\alpha^2 + q^2 B^2} \begin{pmatrix} \frac{qB}{m} - \frac{\alpha}{m} e^{- \frac{\alpha}{m} t} \sin \left (\frac{qB}{m} t \right) - \frac{qB}{m} e^{- \frac{\alpha}{m} t} \cos \left (\frac{qB}{m} t \right) \\ \frac{\alpha}{m} - \frac{\alpha}{m} e^{- \frac{\alpha}{m} t} \cos \left (\frac{qB}{m} t \right) + \frac{qB}{m} e^{- \frac{\alpha}{m} t} \sin \left (\frac{qB}{m} t \right) \end{pmatrix}\]We graph this using Asymptote (because we can).
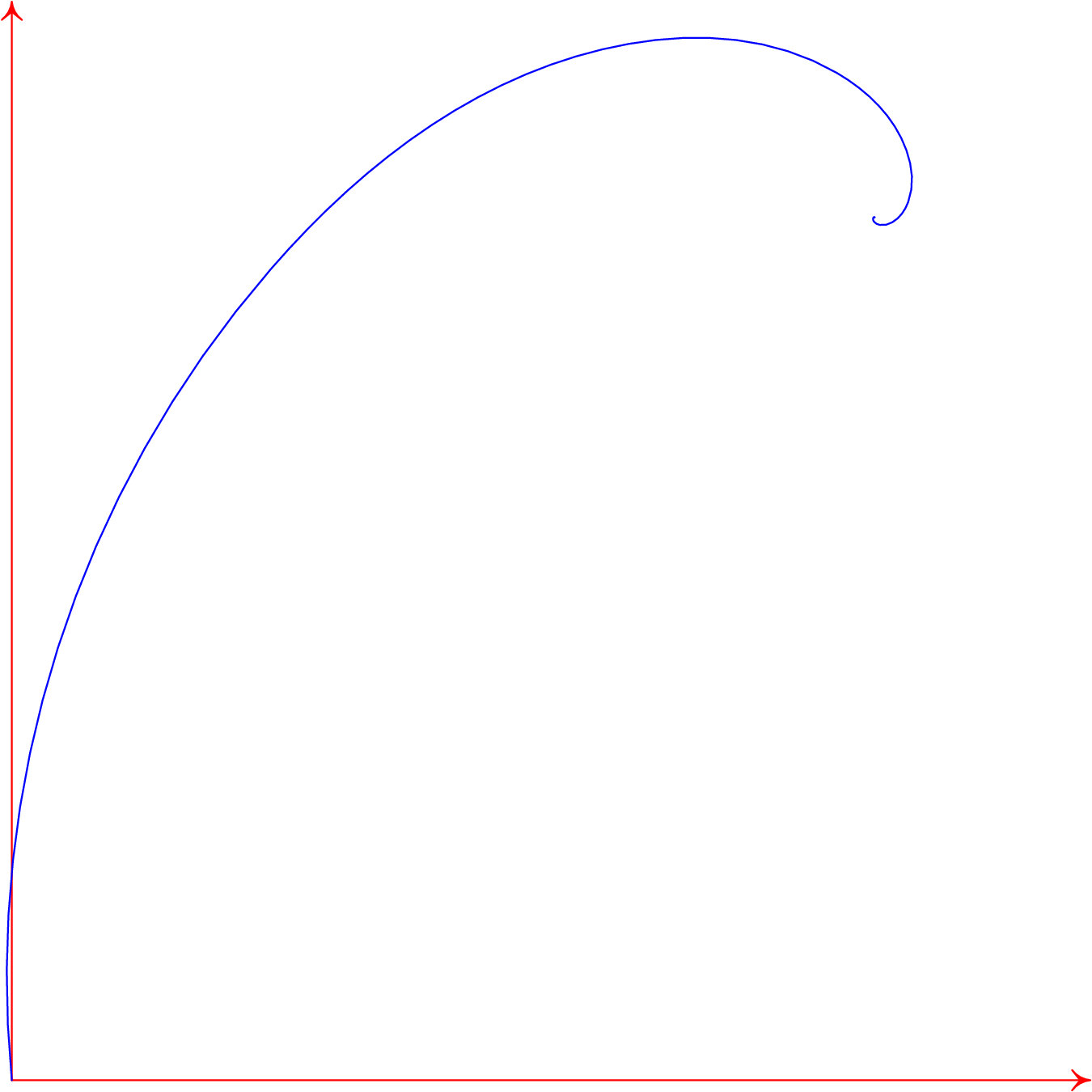
We see that the final position of the particle is at
\[(x, y) = \frac{ v_0}{\left (\frac{\alpha}{m} \right)^2 + \left (\frac{qB}{m} \right)^2 } \left (\frac{qB}{m}, \frac{\alpha}{m} \right)\]